【算法】二叉搜索树的后序遍历序列

题目

输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true，否则返回 false。假设输入的数组的任意两个数字都互不相同。

参考以下这颗二叉搜索树：

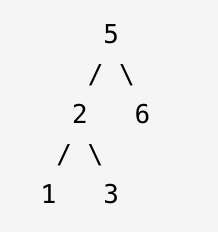
示例 1：

输入: [1,6,3,2,5]
输出: false

示例 2：

输入: [1,3,2,6,5]
输出: true

预备知识点

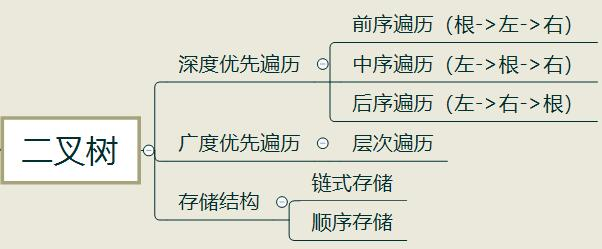
二叉树的遍历

二叉树的深度优先遍历可细分为前序遍历、中序遍历、后序遍历，这三种遍历可以用递归实现，也可使用非递归实现。

前序遍历：根节点->左子树->右子树（根->左->右）

中序遍历：左子树->根节点->右子树（左->根->右）

后序遍历：左子树->右子树->根节点（左->右->根）

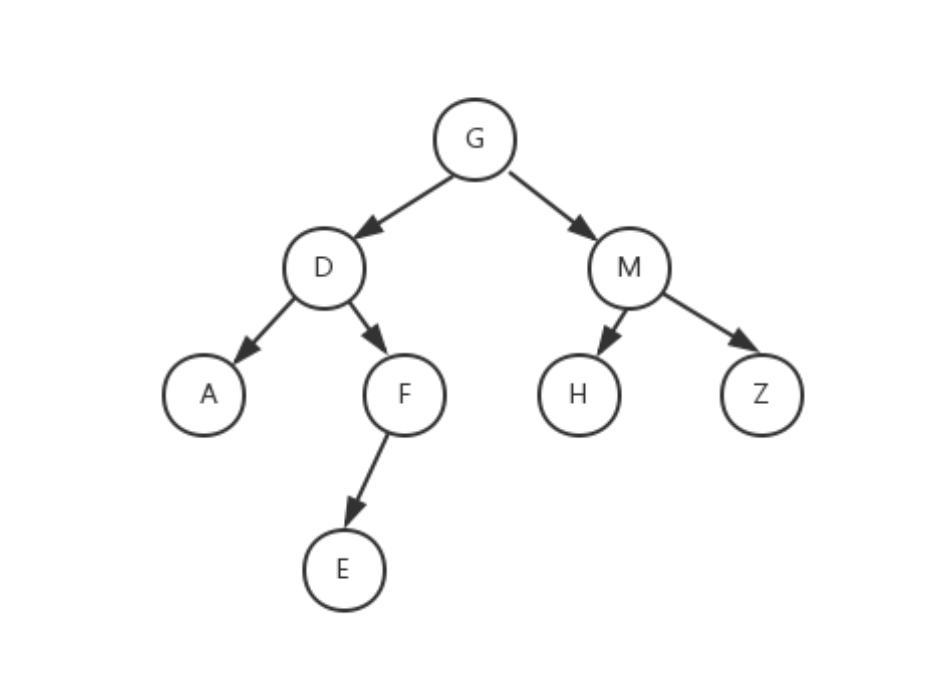
1. 前序遍历

前序的遍历的特点，根节点->左子树->右子树，注意看前序的遍历的代码printf语句是放在两条递归语句之前的，所以先访问根节点G，打印G，然后访问左子树D，此时左子树D又作为根节点，打印D，再访问D的左子树A

A又作为根节点，打印A，A没有左子树或者右子树，函数调用结束返回到D节点（此时已经打印出来的有：GDA）D节点的左子树已经递归完成，现在递归访问右子树F，F作为根节点，打印F，F有左子树访问左子树E，E作为

根节点，打印E，（此时已经打印出来的有：GDAFE），E没有左子树和右子树，函数递归结束返回F节点，F的左子树已经递归完成了，但没有右子树，所以函数递归结束，返回D节点，D节点的左子树和右子树递归全部完成，

函数递归结束返回G节点，访问G节点的右子树M，M作为根节点，打印M，访问M的左子树H，H作为根节点，打印H，（此时已经打印出来的有：GDAFEMH）H没有左子树和右子树，函数递归结束，返回M节点，M节点的左子树已经

递归完成，访问右子树Z，Z作为根节点，打印Z，Z没有左子树和右子树，函数递归结束，返回M节点，M节点的左子树右子树递归全部完成，函数递归结束，返回G节点，G节点的左右子树递归全部完成，整个二叉树的遍历就结束了

前序遍历结果：GDAFEMHZ

总结一下前序遍历步骤

第一步：打印该节点

第二步：访问左子树，返回到第一步（注意：返回到第一步的意思是将根节点的左子树作为新的根节点，就好比图中D是G的左子树但是D也是A节点和F节点的根节点）

第三步：访问右子树，返回到第一步

第四步：结束递归，返回到上一个节点

前序遍历的另一种表述：

（1）访问根节点

（2）前序遍历左子树

（3）前序遍历右子树

（在完成第2,3步的时候，也是要按照前序遍历二叉树的规则完成）

2. 中序遍历（详细遍历过程就不再赘述了，(┬＿┬)）

第一步：访问该节点左子树

第二步：若该节点有左子树，则返回第一步，否则打印该节点

第三步：若该节点有右子树，则返回第一步，否则结束递归并返回上一节点

（按我自己理解的中序就是：先左到底，左到不能在左了就停下来并打印该节点，然后返回到该节点的上一节点，并打印该节点，然后再访问该节点的右子树，再左到不能再左了就停下来）

中序遍历的另一种表述：

（1）中序遍历左子树

（2）访问根节点

（3）中序遍历右子树

（在完成第1，3步的时候，要按照中序遍历的规则来完成）

所以该图的中序遍历为：ADEFGHMZ

3. 后序遍历步骤

第一步：访问左子树

第二步：若该节点有左子树，返回第一步

第三步：若该节点有右子树，返回第一步，否则打印该节点并返回上一节点

后序遍历的另一种表述：

（1）后序遍历左子树

（2）后序遍历右子树

（3）访问根节点

（在完成1,2步的时候，依然要按照后序遍历的规则来完成）

该图的后序遍历为：AEFDHZMG

网上多找一些重构二叉树的练习题，有助于加深理解上述三种遍历树的过程

重要概念

二叉搜索树特征：左子树小于根节点小于右子树

题解思路

理解上述知识点后，回顾题目，既然是后序遍历，那么，数组最后一个一定是根节点，例如给你[1,3,2,6,5]这个数组，那么5就是根节点，按照二叉搜索树的特征，1，3就是左子树，2，6，5就是右子树。同时每个子树也要满足上诉条件，自然而然就想到递归查找判断了。明白了这些原理后，用代码实现就很容易了。

代码实现

/**
 * @param {number[]} postorder
 * @return {boolean}
 */
var verifyPostorder = function(postorder) {
    if (!postorder.length) return true; // 如果没有子树了，返回true
    const root = postorder[postorder.length - 1]; // 后续遍历结果的最后一位是树的根节点
    // 根节点的左子树全部小于根节点，根节点的右子树全部大于根节点
    const leftTree = [], rightTree = []; // 缓存当前节点的左子树和右子树，用于下次递归查询判断
    let cIndex = null; // 记录左右子树的分界点，即第一个满足右子树的节点，因为左右子树要分开递归查
    const flag = postorder.every((item, index) => {
        if (index === postorder.length - 1) return true; // 根节点不判断
        if (cIndex === null && item > root) {
            cIndex = index; // 记录第一个遇到大于根节点的右子树节点，作为分界线
        }
        if (cIndex !== null) { // 如果cIndex !== null，说明已经遍历到右子树的节点了，那就要按照右节点的规则判断接下去的树（右子树的值全都要大于根节点），并且把之后的节点push到右子树的数组，用于递归
            if (index >= cIndex) {
                rightTree.push(item);
                return item > root;
            }
        } else {  // 如果cIndex === null就说名没有遇到右子树的节点，那就判断左子树的特征，左子树的节点都要小于根节点
            leftTree.push(item);
            return item < root;
        }
    })
    if (!flag) return false; // 当前节点都没有满足搜索的特征，那就直接返回false了
    let left = true, right = true;
    if (leftTree.length) {
        left = verifyPostorder(leftTree); // 递归查询判断左子树是否满足二叉搜索树的特征
    } 
    if (rightTree.length) {
        right = verifyPostorder(rightTree); // 递归查询判断右子树是否满足二叉搜索树的特征
    }
    return left && right; // 左右都满足二叉搜索树的特征，才会返回true
};