题目

输入某二叉树的前序遍历和中序遍历的结果，请构建该二叉树并返回其根节点。

假设输入的前序遍历和中序遍历的结果中都不含重复的数字。

示例 1:

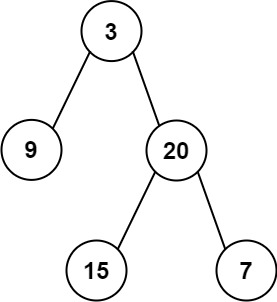
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:

Input: preorder = [-1], inorder = [-1]
Output: [-1]

前置知识

  • 前序遍历列表：第一个元素永远是 【根节点 (root)】
  • 中序遍历列表：根节点 (root)【左边】的所有元素都在根节点的【左分支】，【右边】的所有元素都在根节点的【右分支】

算法思路：

  1. 通过【前序遍历列表】确定【根节点 (root)】
  2. 将【中序遍历列表】的节点分割成【左分支节点】和【右分支节点】
  3. 递归寻找【左分支节点】中的【根节点 (left child)】和 【右分支节点】中的【根节点 (right child)】

题解思路

既然根据前序遍历可以找到根节点，那么构建整个树只要把所有节点都补充起来不就好了？想到树，其实很容易想到递归的思路，因为树的结构是深层次的并且都有规律，根据中序遍历，可以确定左子树跟右子树，那么每次都把左子树跟右子树继续按照第一步的思路来：找到根节点，赋值，继续找左右子树，继续找根节点，赋值…

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {number[]} preorder
 * @param {number[]} inorder
 * @return {TreeNode}
 */
var buildTree = function(preorder, inorder) {
    if (!preorder.length || !inorder.length) {
        return null;
    }
    // 根据前序遍历找到根节点
    const root = preorder[0]; // 根节点就是前序遍历的第一位元素，中序遍历的第二位元素
    const node = new TreeNode(root);
    // 根据中序遍历找到左子树和右子树
    const inorRootIndex = inorder.findIndex(i => i === root);
    const left = inorder.slice(0, inorRootIndex);
    const right = inorder.slice(inorRootIndex + 1, inorder.length);
  	// 左子树中对应的前序遍历元素，左子树的中序遍历元素
    node.left = buildTree(preorder.slice(1, inorRootIndex + 1), left);
  	// 右子树中对应的前序遍历元素，右子树的中序遍历元素
    node.right = buildTree(preorder.slice(inorRootIndex + 1), right);
    return node;
};